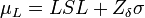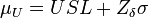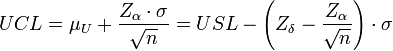Gráficos de Control

Los gráficos de control tienen su origen al final de la década de 1920, cuando Walter A. Shewhart analizó numerosos procesos de fabricación concluyendo que todos presentaban variaciones. Encontró que estas variaciones podían ser de dos clases: una aleatoria, entendiendo por ella que su causa era insignificante o desconocida, y otra imputable (también llamada asignable), cuyas causas podían ser descubiertas y eliminadas tras un correcto diagnóstico.

Los gráficos de control constituyen una herramienta estadística utilizada para evaluar la estabilidad de un proceso. Permite distinguir entre las causas de variación. Todo proceso tendrá variaciones, pudiendo estas agruparse en:

• Causas aleatorias de variación. Son causas desconocidas y con poca significación, debidas al azar y presentes en todo proceso.
• Causas específicas (imputables o asignables). Normalmente no deben estar presentes en el proceso. Provocan variaciones significativas.

Las causas aleatorias son de difícil identificación y eliminación. Las causas específicas sí pueden ser descubiertas y eliminadas, para alcanzar el objetivo de estabilizar el proceso.

Existen diferentes tipos de gráficos de control:

• De datos por variables. Que a su vez pueden ser de media y rango, mediana y rango, y valores medidos individuales.
• De datos por atributos. Del estilo aceptable / inaceptable, sí / no,…

En la base de los gráficos de control está la idea de que la variación de una característica de calidad puede cuantificarse obteniendo muestras de las salidas de un proceso y estimando los parámetros de su distribución estadística. La representación de esos parámetros en un gráfico, en función del tiempo, permitirá la comprobación de los cambios en la distribución.

El gráfico cuenta con una línea central y con dos límites de control, uno superior LCS) y otro inferior (LCI), que se establecen a ± 3 desviaciones típicas (sigma) de la media  (la línea central). El espacio entre ambos límites define la variación aleatoria del proceso. Los puntos que exceden estos límites indicarían la posible presencia de causas específicas de variación.

Los Gráficos de control sirven para poder analizar el comportamiento de los diferentes procesos y poder prever posibles fallos de producción mediante métodos estadísticos. Estas se utilizan en la mayoría de los procesos industriales.

En ciertos procesos en los que se alcanza un alto grado de capacidad es aconsejable reducir el nivel de control proporcionado por los gráficos de control estándar, para ello utilizaremos los límites de control modificados.

Límites de control modificados

Los límites de control modificados para la X_media se utilizan cuando C_p o C_pk es mucho mayor que 1, es decir, cuando la variabilidad del proceso es mucho menor que la extensión de los límites.

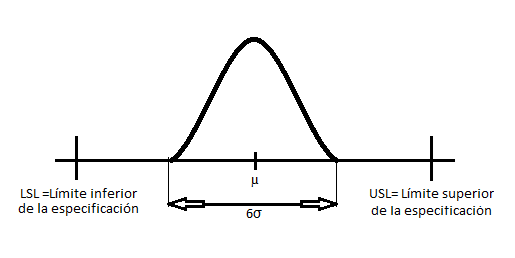
Pongamos, por ejemplo, que nuestro proceso consiste en llenar sacos de arena. Las especificaciones del fabricante exigen que cada saco sea llenado con una cantidad de arena entre los 10.00Kg y los 10.20 Kg. Por otra parte, nuestro proceso puede operar con una variación de 0.01 Kg. Vemos que en este caso la capacidad del proceso es:

En estos casos en los que el intervalo de las especificaciones es tan grande en relación a 6σ se recomienda cambiar de los gráficos de control de X_media habitual a los gráficos modificados. En esta, se permite el desplazamiento de la media un cierto rango, siempre que esta variación no resulte en la aparición de un número significativo de piezas defectuosas, es decir, producir piezas defectuosas con una probabilidad δ. La media se puede desplazar, tanto superior µ_U como inferiormente µ_L, un valor tal que la probabilidad de estar fuera de las especificaciones sea δ. Supondremos que la variabilidad del proceso está bajo control. Para especificar los nuevos límites de control de la carta modificada, tendremos en cuenta que el valor de la media tiene que estar entre µ_U y µ_L, se pueden calcular mediante:

Donde Z_δ representa el punto porcentual superior 100(1-α) de la distribución normal estándar.

Para estimar estos límites lo más común es que la Zα tenga un valor de 3.

Para los gráficos de control modificados debe utilizarse una buena estimación de σ. En los casos en los que la variabilidad en el proceso cambia, los límites de control modificados no son adecuados y en su lugar se debe usar un gráfico R o S.

E ste vídeo ilustra la forma que se pueden hacer los gráficos de control en excel.

Estadística

La estadística es comúnmente considerada como una colección de hechos numéricos expresados en términos de una relación sumisa, y que han sido recopilado a partir de otros datos numéricos.

Kendall y Buckland (citados por Gini V. Glas / Julian C. Stanley, 1980) definen la estadística como un valor resumido, calculado, como base en una muestra de observaciones que generalmente, aunque no por necesidad, se considera como una estimación de parámetro de determinada población; es decir, una función de valores de muestra.

"La estadística es una técnica especial apta para el estudio cuantitativo de los fenómenos de masa o colectivo, cuya mediación requiere una masa de observaciones de otros fenómenos más simples llamados individuales o particulares". (Gini, 1953. Murria R. Spiegel, (1991) dice: "La estadística estudia los métodos científicos para recoger, organizar, resumir y analizar datos, así como para sacar conclusiones válidas y tomar decisiones razonables basadas en tal análisis. 

"La estadística es la ciencia que trata de la recolección, clasificación y presentación de los hechos sujetos a una apreciación numérica como base a la explicación, descripción y comparación de los fenómenos". (Yale y Kendal, 1954). 

Cualquiera sea el punto de vista, lo fundamental es la importancia científica que tiene la estadística, debido al gran campo de aplicación que  posee.

con ayuda del siguiente vídeo se podrá entender mejor el concepto de estadística.